Elements of Newtonian Philosophy (French Translation)

Elements of Newtonian Philosophy (Fr. Elémens de la Philosophie Newtonienne) serves as an invaluable artifact from the Enlightenment era, aimed at disseminating the groundbreaking scientific theories proposed by Sir Isaac Newton. Written by Henry Pemberton, a British physician and mathematician and associate of Newton, this work aims to make Newton's complex ideas in physics and mathematics more accessible to a wider audience.

Henry Pemberton

Henry Pemberton (1694–1771) was an intellectual of considerable standing in his time. A physician by training, he also had a deep interest in mathematics and natural philosophy. He was closely connected to the Royal Society and interacted with leading scientists and thinkers of his era, including Isaac Newton himself, whom Pemberton often edited works for. This background equipped him well to undertake the task of explaining Newtonian philosophy. Given his mathematical training, his rendition is considered to be a technically robust and accurate account of Newton's original works, notably Newton's "Mathematical Principles of Natural Philosophy" ("Philosophiæ Naturalis Principia Mathematica").

The Content of the Book

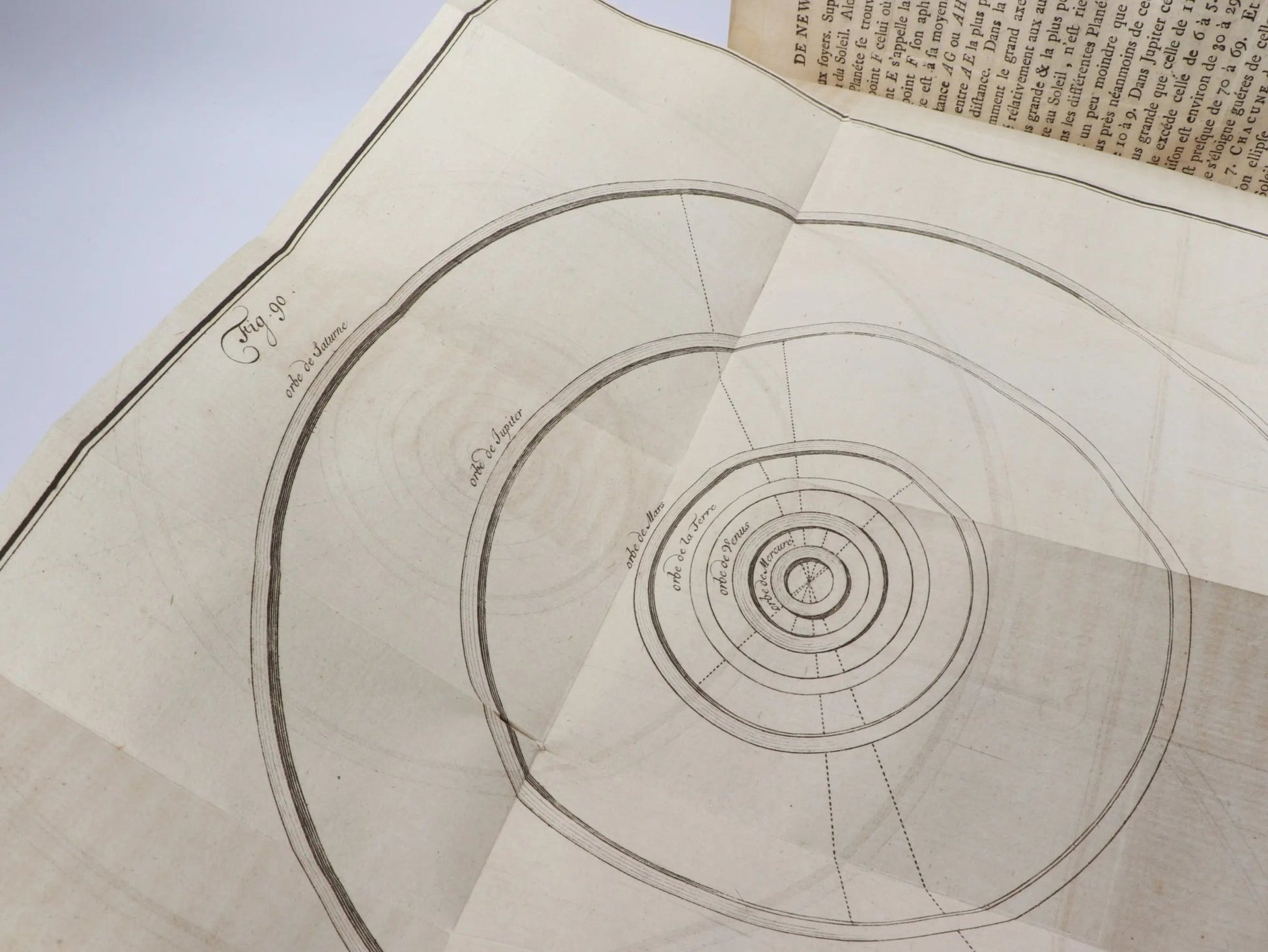
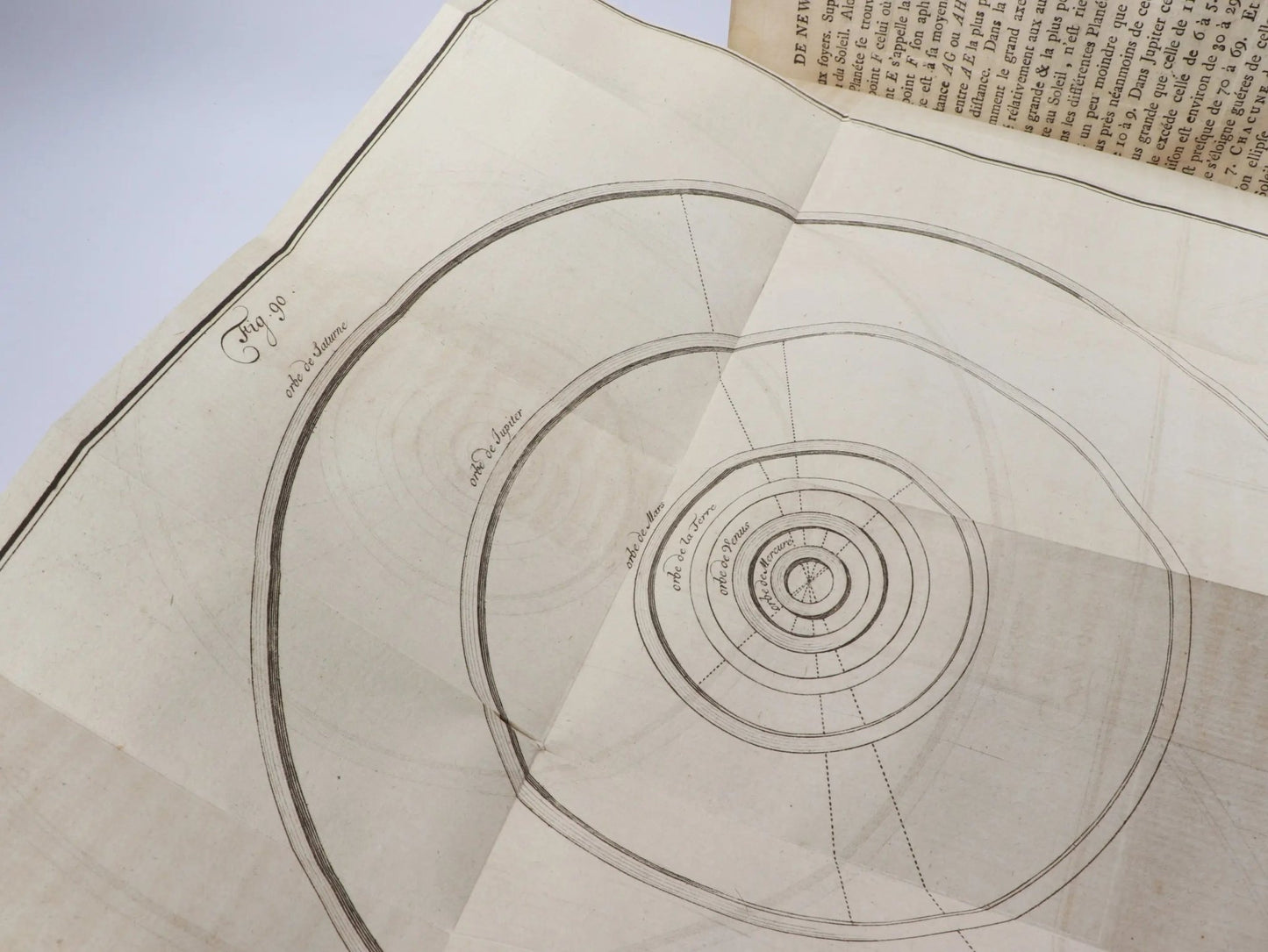
Pemberton's work can be viewed as an expository piece, breaking down Newton's laws of motion, his theory of gravitation, and his work on optics among other topics. It adheres closely to the mathematical and scientific rigor that characterized Newton's original works. Through elaborate explanations, mathematical derivations, and empirical examples, Pemberton aimed to provide a comprehensive understanding of Newtonian physics.

Historical Significance

The book holds considerable historical importance for several reasons:

Popularization of Newtonian Philosophy: One of the primary challenges of the time was the complexity and mathematical depth of Newton's original works. Pemberton's book served as a vital medium to make these theories more comprehensible, thereby increasing their reach.

International Impact: Given that this is the French translation, it's evident that the book aimed to influence not just British intellectual circles but also continental Europe. This aligns with the broader dissemination of Newtonian ideas beyond English-speaking countries.

Scientific Discourse: Works like this served as the catalyst for scientific discussions among intellectuals during the Enlightenment era, driving forward the age's core principles of reason and empirical inquiry.

Educational Utility: Texts like Pemberton's were often used for educational purposes, serving as textbooks or supplementary materials for those studying natural philosophy, thereby impacting subsequent generations of thinkers and scientists.

Elements of Newtonian Philosophy is not merely a book but a historical document that offers significant insights into the transmission and reception of scientific ideas during the Enlightenment. It represents an earnest effort by a qualified contemporary to present and explain the revolutionary scientific theories of Isaac Newton to a broader audience, thereby contributing to the advancement of science and rational thought during a pivotal period in human history.

495 pages
12 folded illustrated diagrams
Condition: Very good

Only 1 available.
Ships free, insured, and packed incredibly safe.